calcSD uses a collection of datasets to make up regional averages. The datasets we use contain researcher-verified measurements with consistent methodology, and we sometimes re-evaluate the datasets currently in use in order to catch potential inaccuracies or biases. With each dataset added/removed, there will be minor changes to the stats. More info about the current datasets is available on the Dataset List page.

Do note that while we display rounded numbers to you, the calculations themselves are used with as many decimal places as allowed by our code, meaning you will get a less accurate percentile result if you try to do the calculations yourself using the rounded average and SD we display. Because of this, you'll also notice that typing in the exact average may not give you back exactly the 50th percentile.

We have two different methodologies to determine the statistics, one for most regular measurements, and one for volume.

Length and Girth Stats

Each measurement (erect length, girth, flaccid length, etc.) has an average and a standard deviation, along with a total number of samples (amount of people measured). To calculate where a certain size belongs in comparison to the average, a z-score (which is a measure of how many standard deviations away from the average you are) is calculated on the fly. The z-score is also known as a standard score.

To understand how z-scores work, if the average length is 13cm and the standard deviation is 1cm, then at 14cm your z-score would be +1 which is one SD above the mean. At 16cm you'd have a z-score of +3, at 11cm you'd have a z-score of -2 and so forth.

Assuming a normal distribution (also known as Gaussian distribution), we can use the following formula to reliably determine the percentile that any z-score would fall onto.

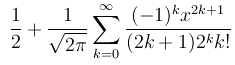
The percentile is the main result given to you by calcSD. Normal distributions are common in nature and tend to be reliable estimates. While we considered the usage of log-normal distribution, these tend to add an excessive right skew to the average which is inconsistent with the included studies's data at both left and right tails. If penis size is not under appreciable selection, then it is likely to be an accurate approximation.

After a percentile is calculated, it's not difficult to use that rarity to compare against a room of n guys in the end. Fun fact: the 0 and 100 percentiles don't exist. Saying you're in the 99 percentile means you're higher than 99% of the population, but saying you're on the 100 percentile means you're higher than 100% of the population, including yourself... which is a contradiction. Same goes for the 0 percentile but in reverse.

We also use the rarity to display size classifications. Where one chooses to place cutoffs for such descriptive classifications is somewhat arbitrary, however for penis size the normal range is medically defined as within 2 SD of the mean, with sizes outside the normal range classified as Abnormally Small or Abnormally Large. Similarly, Micropenis is medically defined as beyond -2.5 SD below the mean, while Macropenis is defined as 2.5 SD above the mean, which each separately correspond to the rarity of ~0.62% of men or an incidence of about 1 in 161 men (technically the definitions of micropenis and macropenis only apply to stretched/erect length, but we may as well apply it to other dimensions too). Additionally, the Statistically Unlikely classification (previously called Theoretically Impossible) is calculated as the size at which the rarity exceeds that of 1 person in the entire global population of males over 15 years of age (~36.8% of 7.7 billion), which corresponds to roughly 6.2 SD from the mean.

Do note that just because a size is determined as impossible in theory, does not mean that it actually is. Biological conditions or just normal genetics can create exceptions in extremely rare cases, much like how the largest human height ever recorded was 8'11", which would be theoretically impossible under the normal approximation to height, since that would be a z-score of well over 12 even when considering just the distribution of heights for men in Western demographics.

This person talks more about how the normal approximation may not be perfect for extreme heights, and hints at a potential issue of our normal distribution's kurtosis and how we might be underestimating the proportions in the extreme tails. The same might also apply to penis size, though with our current data we do not know for sure yet. Regardless, the Statistically Unlikely label offers a rough estimate of the theoretical limit beyond which sizes are not expected to occur in our global population.

Volume Stats

After all that, we estimate statistics for the volume of a penis. The volume of the measurements inserted is calculated using the following formula:

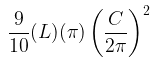
Assuming a perfectly circular girth shape (not the case in real-life), cross-sectional area of the shaft is calculated, then multiplied by the length of the penis to get a cylindrical approximation of the volume. This cylinder is then corrected by multiplying by 0.9 since penises are typically only occupying close to that proportion of a perfect cylinder (obviously this approximation doesn't accurately predict the volume of every penis since some are very non-uniform, however it should on average improve the estimate by correcting for volume reductions from the indentation below the coronal ridge, the conical head, and the imperfectly circular circumference).

The distribution for volume however, is way more complicated. To calculate that, we'd need either paired data of lengths and girths. Unfortunately paired data is not readily available, so the most reliable method of determining volume is already out of the question. We do have studies that have contributed their correlation values between length and girth though, which is still useful.

An alternative is to mix two normal distributions together using a correlation value, thus gaining a multivariate normal distribution. This allows us to create our own pairs of length and girth data based on the existing statistics. Unfortunately, this is still not enough to estimate volume as the volume of 200ml may be achieved with a size of 16.5cm of length by 13cm of girth (which falls slightly outside average range and thus should be commonly expected) but also by a size of 13cm by 14.5cm, which is significantly more uncommon. Calculating the rarity of a specific size then would exclude the rarity of other sizes which may have the same volume.

So, in order to calculate the volume rarity we must calculate the volumes of each of the length and girth pairs generated before and then create a mixture model of the generated volume data. The resulting distribution is very close to a normal distribution, however, it has a right skew which can cause large differences in the tails (for constant length and a normal approximation to the volume, to get the same percentile as the multivariate distribution in some cases it can correspond to more than half an inch less girth). This difference is because the distribution of volume is not normal, which is known from the math behind the product of normal variables.

These calculations are fairly intensive, so they cannot be done on the fly. Instead we have a file containing precalculated volumes for every 0.5ml increment and their relevant percentiles. A separate file is generated for each dataset.

The correlation coefficients used as estimated from studies are:
BPEL - Erect Girth: r = 0.55
NBPEL - Erect Girth: r = 0.40

Regional Averages

Regional averages are actually a type of dataset that calcSD internally calls "aggregates". To join multiple different datasets together, the sample size of each measurement type (length, girth, etc.) is added up. The average and standard deviation of said measurement type in each dataset is then divided by the total amount of samples in all datasets and multiplied by the total amount of samples in that specific dataset. An easy example is detailed over on the old version of calcSD. Note that the calcSD Averages are outdated and no longer used.

We are looking into changing how this data is added up to see if we can improve its accuracy by using a methodology similar to how volume is calculated above: by simulating samples from each dataset, then estimating an average based on the samples created. This or a different methodology, or perhaps multiple different ones, might be used in a future update.